Squeeze and Excitation Networks
At each layer of a convolutional network, a collection of filters expresses local spatial connection patterns along the input channels. This enables CNNs to capture hierarchical patterns and create globally theoretically relevant fields. The convolutional filters create the feature maps using the learned weights in those filters. The filters collectively learn as they analyze the image various feature representations of the target class information included in the image encoded by the input tensor. Some filters pick up edges, while others pick up textures.
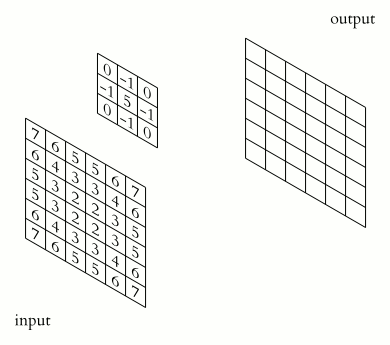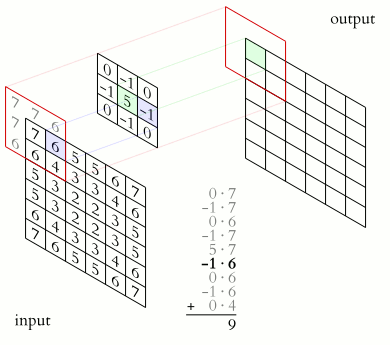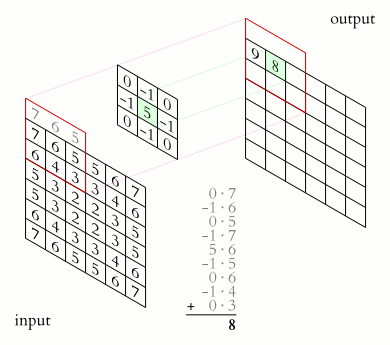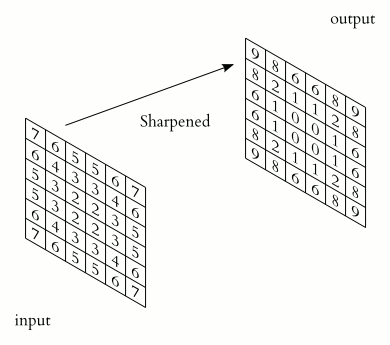 Figure 1: A GIF showing the operation of a convolutional network
Figure 1: A GIF showing the operation of a convolutional network
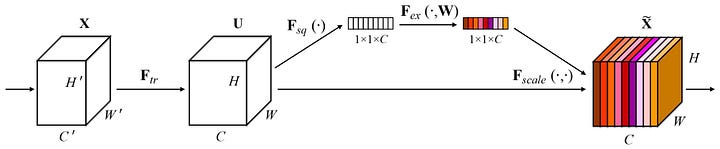
One main problem with such operation is while getting output from the input, we assume each channel is equal in importance. In this article, we examine one use of a novel architecture that Hu et al. 1 described in their study, “Squeeze-and-Excitation.” Squeeze-and-Excitation Networks (SENet) explicitly model the dependencies between the channels of a network’s convolutional features in order to improve the quality of representations produced by the network.
In order to adjust features for SENet to enhance informative parts while suppressing less valuable ones, the network employs a self-attention approach.
2. Squeeze-and-Excitation Blocks (SE Blocks)
A Squeeze-and-Excite block is a brand-new, simple-to-plug-in module.
A Squeeze-and-Excitation block can be built on the top of a transformation mapping an input to features by using a set of filters . We can write output filters as :
where is a learned filter and is the corresponding output for the such filter. All channels are added together to form output; however, the convolution’s channel interactions are implicit and local by nature. By explicitly modeling channel interdependency and raising the network’s sensitivity to informative channels, SENet seeks to improve the quality of feature representation. SE Block consists of two modules:
- Squeeze module
- Excitation module
2.1 Squeeze
It is necessary to use a feature descriptor that can reduce the data from each feature map to a single value to reduce the entire process’s computational complexity. A variety of feature descriptors can be used to reduce the spatial dimensions of feature maps to a single value; however, pooling is a general strategy employed in convolutional neural networks to do so. Average pooling and maximum pooling are two of the most used pooling strategies. The process of merging a feature map into a scalar by averaging its values over predetermined window widths is known as average pooling. On the other hand, max pooling uses the feature map’s maximum value inside a certain window size. The full feature map is the window size for global average pooling (GAP) and global max pooling (GMP), yielding just one scalar value per feature map. The authors did a study comparing the effects of using different techniques and found that GAP works better as a squeeze operation.
Each unit of the transformation’s output is incapable of using contextual data that lies outside the learned filters’ receptive field. In the end, to solve the issue, global average pooling is used by the authors to condense global spatial information into a channel descriptor. Assume the input to the squeeze operation is in the shape of where: is the batch size, and correspond to the height and width of the feature map and corresponds to the total number of channels/feature maps (number of filters applied in the previous layer)
In summary, the squeeze module allows us to transform a feature map into a single scalar representation of the whole map.
2.2 Excitation Module
To fully utilize the information gathered in the squeeze operation, a second operation, excitation, is used to collect channel-wise dependencies. The Excitation module is responsible for learning the adaptive scaling weights for these channels. According to the author, the operation in the excitation module must be: Capable of learning a nonlinear interaction between channels It must learn a non-mutually-exclusive relationship so that multiple channels can be allowed to be emphasized
The author proposes a simple gating mechanism with a sigmoid activation:
where refers to the ReLU function, refers to the sigmoid function, is a shaped weight matrix and is a shaped weight matrix. This matrix, with two fully connected layers and a reduction ratio , generates a bottleneck. The reduction ratio enables us to alter the capacity and computational cost of the network’s SE blocks.

The input is initially encoded into a latent vector. By decreasing the input space to a smaller space determined by the reduction factor, the hidden layer serves as a reduction block. After reduction, the latent vector is enlarged to the input vector’s original size.
Recall from Figure X, that the sigmoid function is used at the last layer. So each value at the output vector is actually a scalar ranging in . Now we have the suitable weights, all left is to apply them which is completely straightforward. Using the output vector of the excitation module :
To sum up, we use an MLP network in the excitation module to learn adaptive scaling weights from the aggregated data. A scalar and a feature map are effectively multiplied channel-wise by the function. The SE block can be viewed as a self-attention function on channels with relationships that go beyond the local receptive fields that convolutional filters are sensitive to since it incorporates input-dependent dynamics by nature. The authors also did an ablation study to observe the effects of reduction ratio and the activation function used in the last layer of the bottleneck network.
3. Plugging SE Blocks Into Networks
Now we know what are SE Blocks and what operations it performs but one important question still exists. How can we add SE Blocks into our networks? The SE block can be included after the non-linearity following each convolution in typical designs such as VGGNet. The authors demonstrate how to integrate SE Blocks into two significant architectures: Residual Networks (ResNet) and Inception Networks (InceptionNet) .
 After the last convolutional layer in an Inception Network, the SE-block is added to every Inception block.
In a Residual Network, the Squeeze-Excitation block is put in after the last convolutional layer in the block before the residual is inserted in the skip connection.
Because of the flexible nature of the SE block, there are various possible ways for it to be integrated into these systems.
After the last convolutional layer in an Inception Network, the SE-block is added to every Inception block.
In a Residual Network, the Squeeze-Excitation block is put in after the last convolutional layer in the block before the residual is inserted in the skip connection.
Because of the flexible nature of the SE block, there are various possible ways for it to be integrated into these systems.
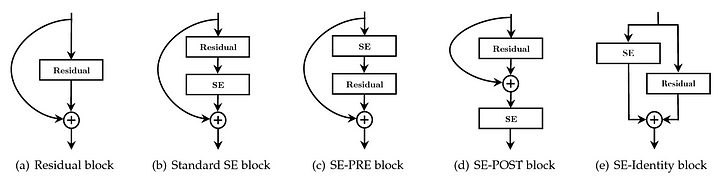 For example, the authors propose four possible strategies to integrate a SE block into ResNet:
For example, the authors propose four possible strategies to integrate a SE block into ResNet:
- Standard SE block is applied immediately after the final convolutional layer of the architecture, just before merging the skip connection
- In SE-PRE configuration the SE block was placed at the beginning of the block
- In SE-POST the SE block was placed at the end of the block
- SE-Identity block is applied to the SE module in the skip connection branch itself in parallel with the main block, and the result is added as a standard residual.
Let’s lok at the effects of SE blocks on the networks. The authors explain the significance of their model by showing that they ranked first in the ILSVRC 2017 classification competition. Their best model ensemble achieves a 2.251% top-5 error on the test set. This represents roughly a 25% relative improvement when compared to the winning entry of the previous year. To prove their result is not limited to a single dataset, the authors provided benchmarks for multiple datasets.
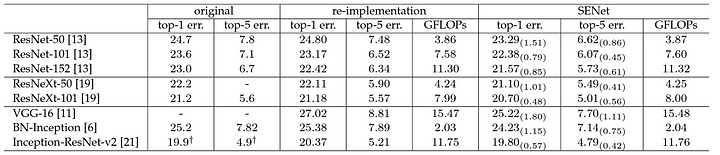 It is clear that adding SE blocks to the network significantly improves performance on all tested networks while only introducing a little amount of model complexity.
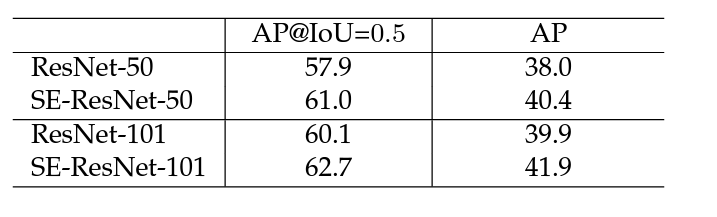
Following table also shows that their results are neither limited to a single task nor to a single dataset.
It is clear that adding SE blocks to the network significantly improves performance on all tested networks while only introducing a little amount of model complexity.
Following table also shows that their results are neither limited to a single task nor to a single dataset.
 Overall, SE blocks are an excellent, basic, and straightforward technique to add self-attention into the model. By squeezing the matrix into a more miniature representation and using this representation to weight the feature maps, we can learn what traditional convolution networks cannot learn.
Overall, SE blocks are an excellent, basic, and straightforward technique to add self-attention into the model. By squeezing the matrix into a more miniature representation and using this representation to weight the feature maps, we can learn what traditional convolution networks cannot learn.
4. Conclusion
The SE block enhances a network’s representational power by allowing it to undertake dynamic channel-wise feature recalibration. The authors of the original research demonstrated that SE blocks are quite effective and may be included in networks to improve results with the cost of increasing model complexity slightly.
Footnotes
-
Jie Hu, Li Shen, Samuel Albanie, Gang Sun, Enhua Wu: “Squeeze-and-Excitation Networks”, 2017; arXiv:1709.01507. ↩